
A triangle that has all interior angles measuring less than 90° is an acute triangle or acute-angled triangle.Triangles that do not have an angle that measures 90° are called oblique triangles.Special right triangles are right triangles with additional properties that make calculations involving them easier. Right triangles obey the theorem: the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse: a 2 + b 2 = c 2, where a and b are the lengths of the legs and c is the length of the hypotenuse. The other two sides are the legs or catheti (singular: cathetus) of the triangle. The side opposite to the right angle is the hypotenuse it is the longest side in the right triangle. A right triangle (or right-angled triangle, formerly called a rectangled triangle) has one of its interior angles measuring 90° (a right angle).Triangles can also be classified according to their internal angles, measured here in degrees.
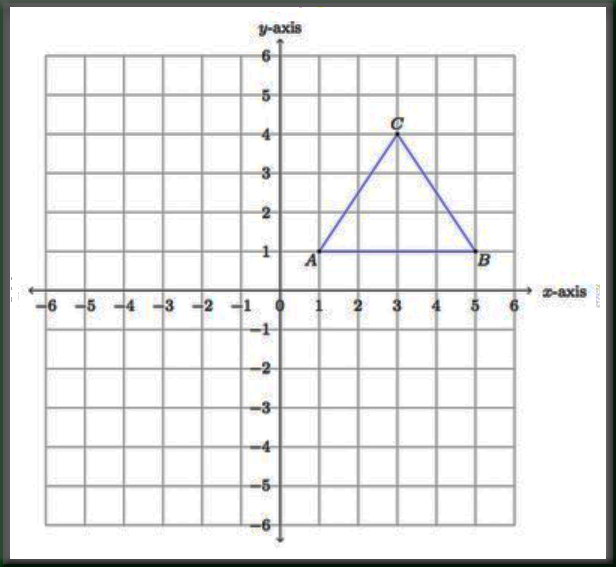
In a scalene triangle, all sides and internal angles are different from one another.(Traditionally, only two sides equal, but sometimes at least two.) An isosceles triangle also has two angles of the same measure namely, the angles opposite to the two sides of the same length. In an isosceles triangle, two sides are equal in length.An equilateral triangle is also a regular polygon with all angles measuring 60°. In an equilateral triangle, all sides have the same length.
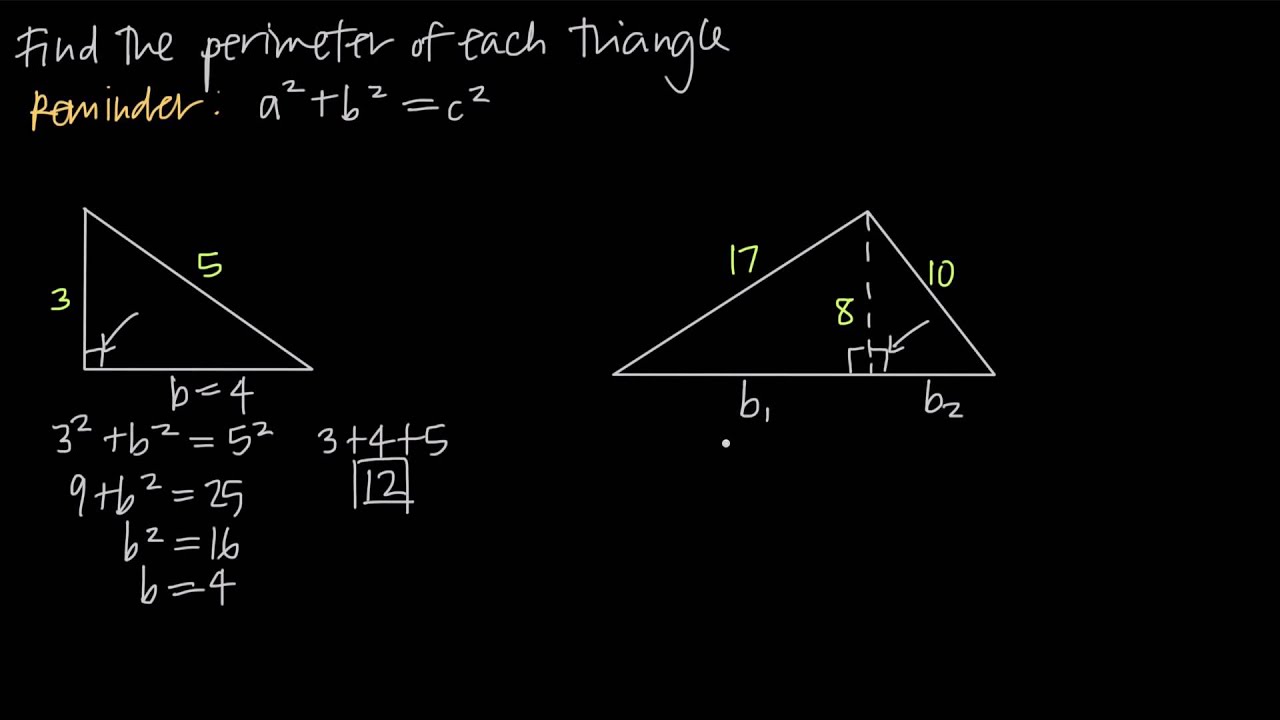
Triangles can be classified according to the relative lengths of their sides: Types of triangles By relative lengths of sides 5.1 Trigonometric ratios in right triangles.


 0 kommentar(er)
0 kommentar(er)
